Back in the 1970s, Apollo's 13 crew aborted their lunar landing due to a explosion in one of the oxygen tanks. Using the following data, our task is to... rescue the astronauts!
| Description | Value |
|---|---|
| Earth's mass | $5.97 \times 10^{24} \; kg$ |
| Earth's radius | $6.378 \times 10^{6} \; m$ |
| Universal Gravitational Constant | $6.67 \times 10^{-11} \; m^3/(kg \cdot s^2)$ |
| Moon's mass | $7.35 \times 10^{22} \; kg$ |
| Moon's radius | $1.74 \times 10^6 \; kg$ |
| Distance from Earth to Moon (not a constant in real life) | $400.5 \times 10^{6} \; m$ |
| Moon's period | $27.3$ days |
| Initial's moon angle | $-61^\circ$ |
| Trip total's length | $12$ days |
| Initial's ship position ($t = 0$) | $[-6.701 \times 10^6, 0]^T \; m$ |
| Initial's ship velocity (at $t = 0$) | $[0, -10.818 \times 10^3]^T \; m/s$ |
Simulate
- An (instantaneous) speed reduction of $7.04$ m/s at 101,104 seconds.
- An (instantaneous) speed increase, given by the
boost(in m/s), at 212.100 seconds. Try with the followingboostvalues: $-10.0$, $10.0$, $50.0$, $100.0$.
Assume the Earth is at the center of a 2-dimensional plane. Consider that Moon's movement is a "perfect" circular translation around the Earth (please, notice we are making a lot of simplifications here, to keep things simple for illustration and blogging purposes).

Using the Universal Gravitational Law, and Newton's 2nd. law, it is possible to get a second order differential equation, explicit, and non-linear, that computes the spaceship acceleration with:
$$\ddot{\mathbf{x}}_n = -G \frac{m_T}{\| \mathbf{x}_n \|^3} \mathbf{x}_n + G \frac{m_L}{\| \mathbf{x}_L - \mathbf{x}_n \|^3} (\mathbf{x}_L - \mathbf{x}_n)$$where $\mathbf{x}_n$ is the spaceship positions (relative to Earth); $m_T$, the mass of the Earth; $G$, Universal Gravitational constant; $m_L$, Moon's mass; $\mathbf{x}_L$ is moon's position.
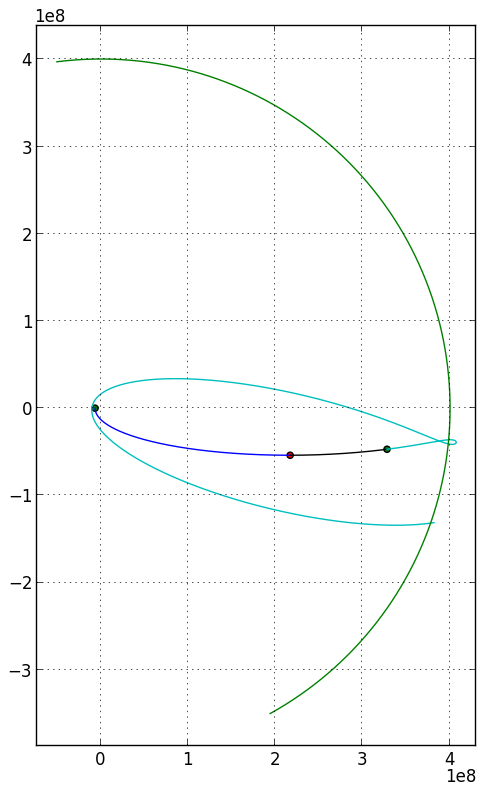
A solution of the route followed by the spaceship could look like the following.